Machine Learning and Data Science are all about playing with numbers. In this blog, I'll be covering some basic mathematical functions/terms that can help you in data analysis.

Logarithm

Imagine you have to visualize the following table

Company	Revenue
Tesla	31
Uber	11
Amazon	386
Jindal Steel	4.7
Axis Bank	5.6
Vedanta	11.3

Plotting this through a bar plot, this is what we'll get

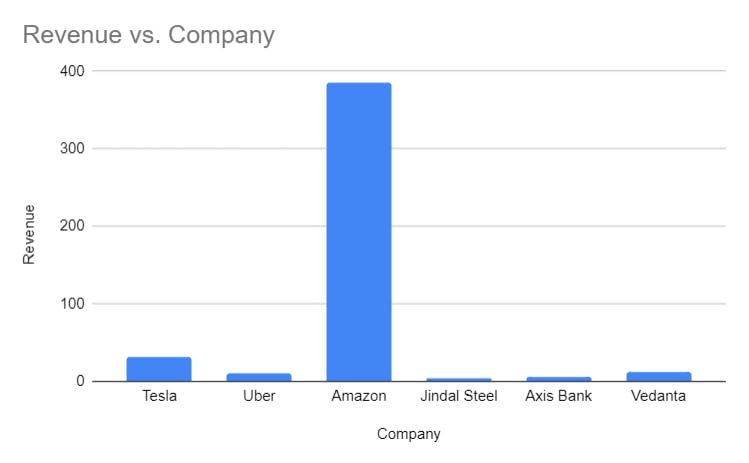
We can see that Amazon have such a high revenue that it is making it difficult to read the revenue for Jindal Steel and Axis Bank. So what we do now, here comes the concept of log. The Log is the inverse of an exponent. In the given equation -

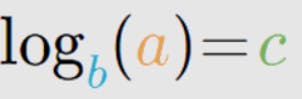
this means that b raised to the power c gives us a*,* where b is the base. The common base used is a base of 10. So in the above data, if I add a column for log base 10, this is what we'll get

Company	Revenue	Log (base 10)
Tesla	31	1.491361694
Uber	11	1.041392685
Amazon	386	2.586587305
Jindal Steel	4.7	0.6720978579
Axis Bank	5.6	0.748188027
Vedanta	11.3	1.053078443

We can see that in the log column, the numbers are very much comparable so as its plot, we can clearly see the difference in revenue of the companies in much better way than the above.

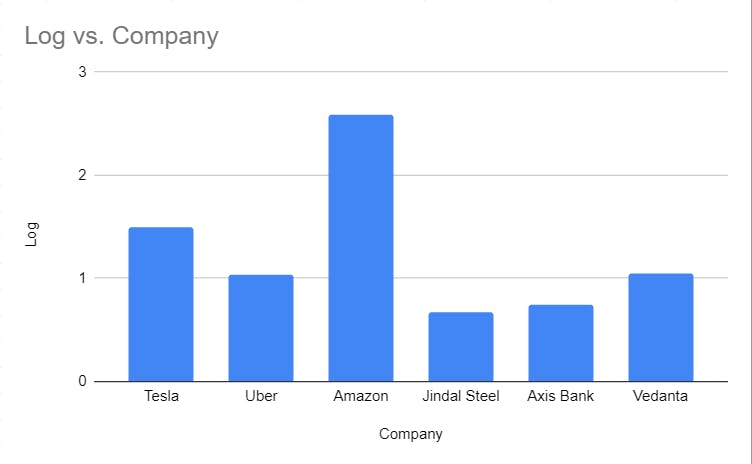
In the log, every consecutive number is base times greater than the preceding one, for example, log₅125 is 10 times greater than log₅25.

Practical examples include Earthquakes, where on a Richter Scale 5 is 10 times more powerful than 4.

Mean and Deviations

Consider the following data on salaries for employees -

Employee Name	Salary (in USD)
Jack	1678.3
Alan	2242.9
Kelvin	998.8
Jake	1938.6
Elly	1200.4

We can say that the average salary of a company is 1611.8 USD, but there is a huge difference between the salary of Kelvin and Alan when compared to the average. Imagine we have a new employee Addie with a salary of 25000 USD and then our new mean salary would be 5509.83 USD, but this isn't the case. We see except 1, everyone has their salary less than 2500 USD. So we can calculate the deviation from mean -

Employee Name	Salary (in USD)	Deviation (Abs)
Jack	1678.3	3831.533333
Alan	2242.9	3266.933333
Kelvin	998.8	4511.033333
Jake	1938.6	3571.233333
Elly	1200.4	4309.433333
Addie	25000	-19490.16667

We see there is a lot of deviation from the mean salary. Now how to sum this up in a single number?

Average won't work, because we have negative values here, so instead of normal averaging, we can square the numbers, add them, divide by the total number of samples, and then square root. This is called Standard Deviation.

Employee Name	Salary (in USD)	Deviation (Abs)	Deviation Sq.
Jack	1678.3	3831.533333	14680647.68
Alan	2242.9	3266.933333	10672853.4
Kelvin	998.8	4511.033333	20349421.73
Jake	1938.6	3571.233333	12753707.52
Elly	1200.4	4309.433333	18571215.65
Addie	25000	-19490.16667	379866596.7
Mean			8726.343666

We can see here that there is so much deviation from the mean salary here..