We have been hearing about machine learning for a long time. IBM defines Machine Learning as a "Branch of artificial intelligence (AI) and computer science which focuses on the use of data and algorithms to imitate the way that humans learn, gradually improving its accuracy"

We categorize ML as Supervised, Unsupervised and Reinforcement Learning. All these types have many Algorithms under them. Every algorithm has its own maths behind its work.

I am exploring this world of applied Mathematics for the last 2 years as an absolute beginner. Starting from concepts of Regression, and exploring algorithms like SVM, decision tree and advanced algorithms such as Random forest, there is rigorous mathematics involved. But there is a very basic equation being followed in most of the algorithms, i.e.

$$y = mx + c$$

You might have studied this in your high school under the topic Equation of Straight Line. This is the very basic equation to determine the equation of the straight line. In this blog, we'll see how this equation is modified in different algorithms and how they work to provide accurate output.

x - Independent Variable

y - Dependent Variable

Simple Linear Regression -

It is the type of regression that shows how two variables (x and y) are changing. We have points on the XY plane and we fit a line across all the points such that the distance between the points and the line is minimum. Here is an example.

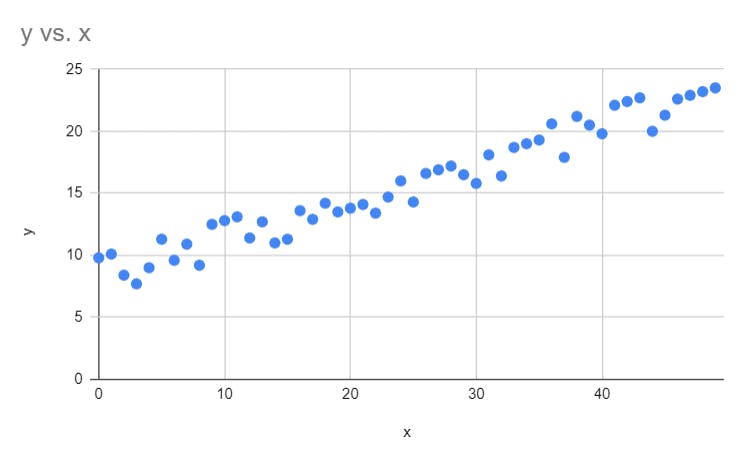
We see the y and x are increasing linearly, so we can fit a line like this and find the values of m and c defining the slope and intercept respectively.

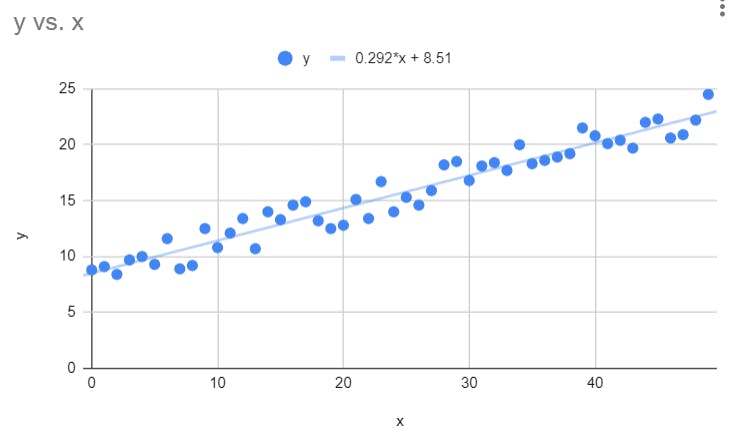
This is a very simple example. That can predict the value of y as per the value of x.

Multiple Linear Regression -

The above simple example gave us the idea of how to find a relationship between two variables. Instead of a single independent variable x, what if we have multiple values of x i.e. my output depends on multiple variables? In that case, we will have a messy graph like this

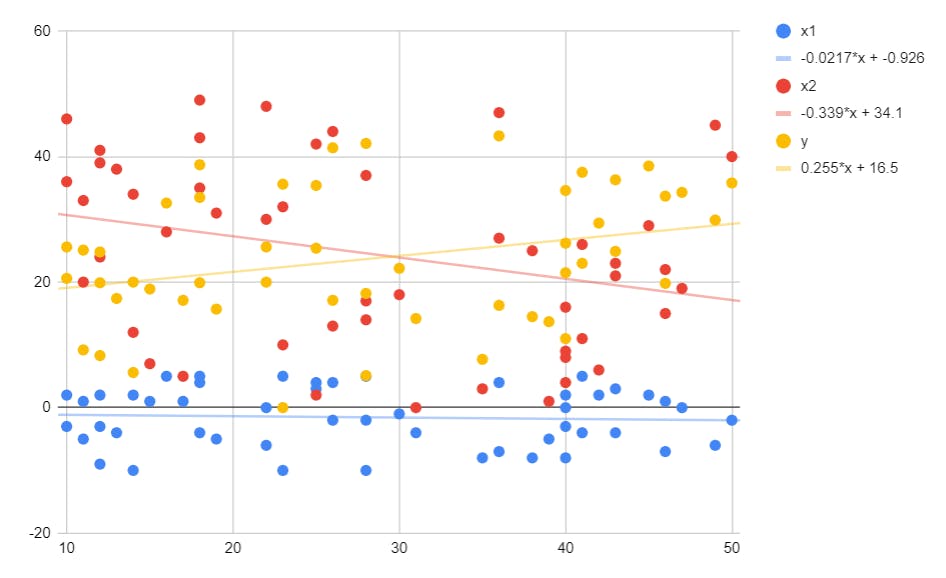
We see three variables here with 3 different lines fit. Here we have multiple values of x and an intercept. Here the equation is like this.

$$y = x{1}m{1} + x{2}m{2} + x{3}m{3} + c$$

Note here that for every independent variable, we have a different slope. We can generalize the equation here as-

$$y = \sum{i=1}^{n}x{i}m_{i} + c$$

Neural Networks

You might be surprised, but actually, the neural network works on this slope-intercept equation. But the twist is, we have to work with different equations at different times.

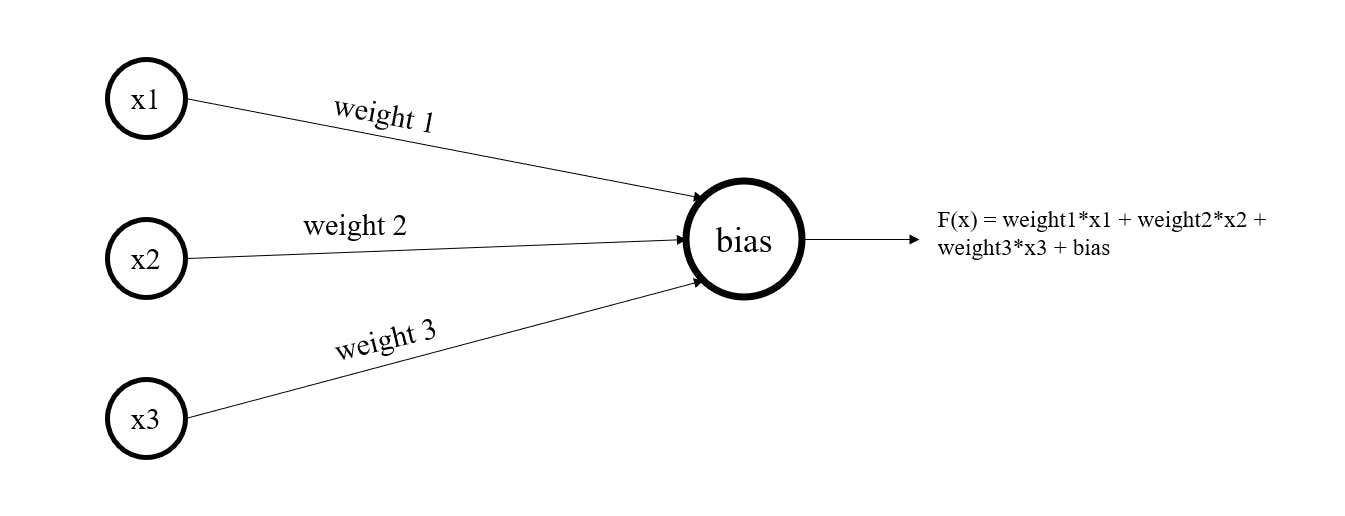
We see that at the end, we have an equation something similar to the above in Multiple Linear Regression. In a complex neural network, we have multiple biases, these biases will continue till we reach the output layer.

Here I have discussed three major use cases of this equation. But there are numerous use cases. For any queries, feel free to comment or contact me over email. Don't forget to subscribe on my website - lakshaykumar.tech